lunes, 15 de febrero de 2010

Bandas de Landau


La teoría de Ginzburg-Landau encuentra su principal aplicación en el estudio de los superconductores no convencionales (muchos de los cuales, si bien no todos, se conocen como superconductores sucios debido a que se caracterizan por su contenido de impurezas), entre los que encontramos los famosos superconductores de alta temperatura.
La razón de ello es que, aunque la teoría más precisa, que es la teoría BCS, explica con éxito muchos detalles de diferentes superconductores (en especial aquellos casos en los que el valor la banda prohibida Δ es constante en todo el espacio), esta no siempre es aplicable. De hecho, en muchos casos todo el interés se basa en la inhomogeneidad de la muestra. La teoría BCS es una teoría microscópica y por ello a veces los problemas que hay que afrontar resultan intratables por ser demasiado complejos, y es aquí donde la única salida es emplear la teoría Ginzburg-Landau.

 


Forma que tiene la energía libre en función de la pseudofunción de onda dependiendo de los parámetros α (que puede ser positivo o negativo) y β (que se toma siempre positivo). El caso más interesante se da cuando α es negativo, ya que entonces encontramos un rango de la pseudofunción para el que la energía libre del estado superconductor es inferior a la del estado normal.
La teoría de Ginzburg-Landau es en cierto modo una generalización de las ideas de los hermanos London y se desarrolla en la línea de la teoría de Landau (no confundir la teoría de Landau, que es una teoría sobre las transiciones de fase en general, con la aquí tratada teoría de Ginzburg-Landau que trata de las transiciones de fase entre el estado superconductor y el normal).
Las hipótesis de partida de la teoría son:

  • La pseudofunción de onda: el supercondensado se puede explicar con la ayuda de una función de onda \Psi(\vec{r}) que en general es compleja, conocida como función de onda de Ginzburg-Landau, o bien parámetro de orden complejo (si bien no se trata de una función de onda en el sentido mecanocuántico, sino de una pseudofunción de onda macroscópica).
  • La densidad de pares: el valor absoluto de dicha pseudofunción de onda nos da la densidad de pares de Cooper:
n_s = |\Psi(\vec{r})|^2.
Históricamente, Ginzburg y Landau, desconociendo que los portadores de carga eran pares de Cooper (lo cual sería explicado siete años más tarde en la teoría BCS), tomaron ns como la densidad de electrones en estado superconductor; sin embargo esto da lugar a muchos problemas, dado que al ser fermiones no puede haber dos en el mismo estado cuántico. Estos problemas desaparecen cuando usamos pares de Cooper, ya que son bosones puesto que se trata de parejas de electrones.
  • La pseudofunción de onda varía poco: \Psi(\vec{r}) no cambia apreciablemente dentro de una distancia del orden de ξ, conocida como longitud de coherencia.
  • Dentro del marco de la mecánica cuántica: la pseudofunción de onda tiene que obedecer ciertas ecuaciones de la mecánica cuántica.

Energía libre y método variacional

La herramienta principal de la teoría es el método variacional aplicado sobre un desarrollo en serie de la energía libre en función de la pseudofunción de onda \Psi(\vec{r}). Ginzburg y Landau asumieron que la energía libre se podía expresar de la siguiente forma:
F = F_n + \alpha |\psi|^2 + \frac{\beta}{2} |\psi|^4 + \frac{1}{2m} \left| \left(-i\hbar\nabla - 2e\vec{A} \right) \psi \right|^2 + \frac{|\vec{B}|^2}{2\mu_0}
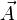donde Fn es la energía libre en la fase normal, α y β son parámetros que se pueden calcular mediante experimentos, m es la masa efectiva, \vec{A} es el potencial vector y \vec{B} es la inducción magnética.
Para ver la situación, podemos observar que en ausencia de campos magnéticos y con gradiente nulo, la diferencia entre la energía libre en el estado superconductor y en el estado normal es:

F_s - F_n = \alpha | \Psi |^2 + \frac{1}{2}\beta|\Psi|^4
Como se puede observar en la gráfica adjunta, tomando β positivo y suponiendo que α sea negativo, habrá un rango del parámetro de orden para el cual la energía es inferior en el estado superconductor.

Las ecuaciones de Ginzburg-Landau

Minimizando la energía libre con respecto a las fluctuaciones del parámetro de orden y el potencial vector, se puede llegar a las ecuaciones de Ginzburg-Landau: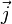

\alpha \psi + \beta |\psi|^2 \psi + \frac{1}{2m} \left(-i\hbar\nabla - 2e\vec{A} \right)^2 \psi = 0
\vec{j} = \frac{2e}{m} Re \left\{ \psi^* \left(-i\hbar\nabla - 2e \vec{A} \right) \psi \right\}
donde \vec{j} es la densidad de corriente y Re significa parte real.
Las ecuaciones de Ginzburg-Landau, entre otras cosas, son importantes porque nos brindan dos cantidades fundamentales en nuestra comprensión de la superconductividad:

  • La longitud de coherencia de Ginzburg-Landau ξ(T) (no confundir con la longitud de coherencia de Pippard ξ0, que prácticamente no depende de la temperatura), la cual nos indica la magnitud de las fluctuaciones termodinámicas en la fase superconductora:
\xi(T) = \sqrt{\frac{\hbar^2}{2 m |\alpha(T)}}

Dependencia del campo magnético interno de un superconductor con respecto al campo magnético externo, el cual varía en función del parámetro de Ginzburg-Landau.



  • La longitud de penetración de Ginzburg-Landau λ (no confundir con la longitud de penetración de London), que es la profundidad hasta la que llega a penetrar un campo magnético en una muestra en fase superconductora:
\lambda = \sqrt{\frac{m}{4 \mu_0 e^2 \psi_0^2}}
Si calculamos el cociente entre estas dos longitudes, obtnemos lo que se conoce como el parámetro de Ginzburg-Landau:

\kappa = \frac{\lambda}{\xi}
el cual es clave para distinguir entre los superconductores de tipo I y los de tipo II, ya que, como demostró Abrikósov (que fue quien propuso este criterio para la clasificación de los superconductores en 1957 en un famoso artículo[4] [5] ), obtenemos que:

  • si \kappa < 1/\sqrt{2} (especialmente, si \kappa \ll 1) entonces la energía superficial del superconductor es positiva y se trata de un superconductor de tipo I,
  • si \kappa> 1/\sqrt{2} (especialmente, si \kappa \gg 1) entonces la energía superficial del superconductor es negativa y se trata de un superconductor de tipo II.

La longitud de coherencia en función de las impurezas

Yendo un poco más lejos, y con la ayuda de la teoría BCS, vemos que se puede decir que cuando T ≈ Tc :
\xi(T) = 0.741 \frac{\xi_0}{\sqrt{1-T/T_c}}, para un superconductor puro (sin impurezas), y
\xi(T) = 0.855 \sqrt{\frac{\xi_0 l}{1-T/T_c}}, para un superconductor sucio, siendo l el recorrido libre medio entre impurezas (por lo que cuantas más impurezas tenga la muestra, más corta será la l y más corta será a su vez la longitud de coherencia).
Esto es así debido a que se puede concluir que[6]

\frac{\xi(T)}{\xi_0} = \frac{\pi}{2 \sqrt{3}} \frac{H_c(0)}{H_c(T)} \frac{\lambda_L(0)}{\lambda_{eff}(T)}
de donde concluimos los resultados previos simplemente sustituyendo las cantidades que predice la teoría BCS:

H_c(T/T_c) = 1.73 H_c(0)(1-T/T_c) \!
\lambda_L(T/T_c) = \frac{\lambda_L(0)}{\sqrt{1-T/T_c}}
\lambda_{eff}(T/T_c) = \lambda_L(T/T_c) \sqrt{\frac{\xi_0}{1.33 l}} (para un superconductor sucio)
Así, es fácil hallar el parámetro de Ginzburg-Landau en cada caso,

\kappa = 0.96 \frac{\lambda_L(0)}{\xi_0}, para un superconductor puro, y
\kappa = 0.715 \frac{\lambda_L(0)}{l}, para un superconductor sucio.
Puesto que el recorrido libre medio entre impurezas l disminuye con la cantidad de impurezas, vemos que cuantas más impurezas contenga la muestra, mayor será el parámetro κ. Llegará un momento en que \kappa> 1/\sqrt{2}, con lo que el superconductor pasará a ser de tipo II, lo cual explica por qué este tipo de superconductores suelen ser sustancias muy complejas constituidas por varios elementos diferentes.


En Física, el Amortiguamiento de Landau, llamado así debido a que fue descubierto por el físico ruso Lev Davidovich Landau, es el efecto de amortiguamiento (disminución exponencial en función del tiempo) de ondas de Langmuir (ondas electrostáticas longitudinales) en un plasma.

Interacción Onda-Partícula

El amortiguamiento de Landau ocurre debido al intercambio de energía entre una onda con velocidad de fase vph, y las partículas con velocidad aproximadamente igual a vph, o sea, que están en resonancia con la onda. Las partículas con velocidad un poco menor que vph serán aceleradas por el campo eléctrico de la onda, es decir, ganarán energía de la onda, mientras que las partículas con velocidad un poco mayor a vph serán desaceleradas por el campo eléctrico, es decir, van a ceder energía a la onda.


Dist maxwell partic resonant.png

En un plasma sin colisiones donde la función de distribución de las velocidades de las partículas sea Maxweliana, se observa que el número de partículas que tienen velocidad un poco menor que la onda es mayor que el número de partículas con velocidad un poco mayor que la onda. Esto quiere decir que hay más partículas obteniendo energía de la onda que partículas cediendo energía a la onda, lo que produce el amortecimiento de la onda.

 

La demostración matemática del amortecimiento de Landau es bastante compleja y envuelve la evaluación de integrales de contorno, pero existe una interpretación física que, a pesar de no ser exacta, facilita enormemente la visualización de este fenómeno.

Phys interp landau damp.png

Podemos imaginar a las ondas de Langmuir como olas en el mar, y las partículas como surfistas, desplazándose en la misma dirección que las olas. Un surfista que se desplace por el agua a una velocidad un poco menor que las olas eventualmente será empujado por una de ellas (gana energía), mientras que un surfista que se desplace un poco más rápido que una ola (tal vez braceando recostado en su tabla, tratando de alcanzar la ola) va a "empujar" la ola (o sea, transfiere energía).
Observese que sólo los surfistas participan en esta interacción de energía con la ola, ya que poseen una velocidad cercana (un poco menor o mayor) a la ola (partículas resonantes). Una pelota flotando en el agua subirá y bajará siguiendo la forma de la ola, sin existir intercambio neto de energía (ni gana ni pierde). Lo mismo ocurre con una lancha desplazándose velozmente por el agua.
¡Nuevo MSN Entretenimiento! Todos los trailers, series de tv y videoclips, los mejores juegos online y lo último sobre tus estrellas favoritas.
Publicado por en
Etiquetas:

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)